lr_scheduler.CosineAnnealingLR¶

class lucid.optim.lr_scheduler.CosineAnnealingLR(optimizer: Optimizer, T_max: int, eta_min: float = 0.0, last_epoch: int = -1, verbose: bool = False)¶

The CosineAnnealingLR learning rate scheduler adjusts the learning rate using a cosine function, allowing for gradual reduction while resetting at T_max epochs. This approach is particularly effective in scenarios where cyclic learning rates improve convergence.

Class Signature¶

class CosineAnnealingLR(
    optimizer: Optimizer,
    T_max: int,
    eta_min: float = 0.0,
    last_epoch: int = -1,
    verbose: bool = False
)

Parameters¶

optimizer (Optimizer): The optimizer whose learning rate needs to be scheduled.
T_max (int): Number of epochs before the learning rate is reset.
eta_min (float, optional): The minimum learning rate. Default: 0.0.
last_epoch (int, optional): The index of the last epoch when resuming training. Default: -1.
verbose (bool, optional): If True, logs learning rate updates at each step. Default: False.

Mathematical Formula¶

The learning rate at epoch \(t\) is computed as:

\[\eta_t = \eta_{\min} + (\eta_0 - \eta_{\min}) \cdot \frac{1 + \cos(\frac{\pi t}{T_{\max}})}{2}\]

Where: - \(\eta_t\) is the learning rate at epoch \(t\). - \(\eta_0\) is the initial learning rate. - \(\eta_{\min}\) is the minimum learning rate. - \(T_{\max}\) is the maximum epoch count before resetting.

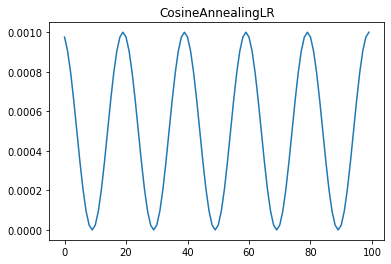
Methods¶

get_lr() -> list[float]: Computes the updated learning rate(s) using cosine annealing.
step(epoch: Optional[int] = None) -> None: Updates the learning rate based on the current epoch.

Usage Example¶

import lucid.optim as optim
from lucid.optim.lr_scheduler import CosineAnnealingLR

optimizer = optim.SGD(model.parameters(), lr=0.1)
scheduler = CosineAnnealingLR(optimizer, T_max=50, eta_min=0.01)

for epoch in range(100):
    optimizer.step()
    scheduler.step()
    print(f"Epoch {epoch+1}, Learning Rate: {scheduler.last_lr}")

Note

CosineAnnealingLR is particularly useful in scenarios where gradual learning rate decay with periodic resets improves training efficiency and convergence.