DDPM¶

Diffusion Image Generation

class lucid.models.imggen.DDPM(model: Module | None = None, image_size: int = 32, channels: int = 3, timesteps: int = 1000, diffuser: Module | None = None, clip_denoised: bool = True)¶

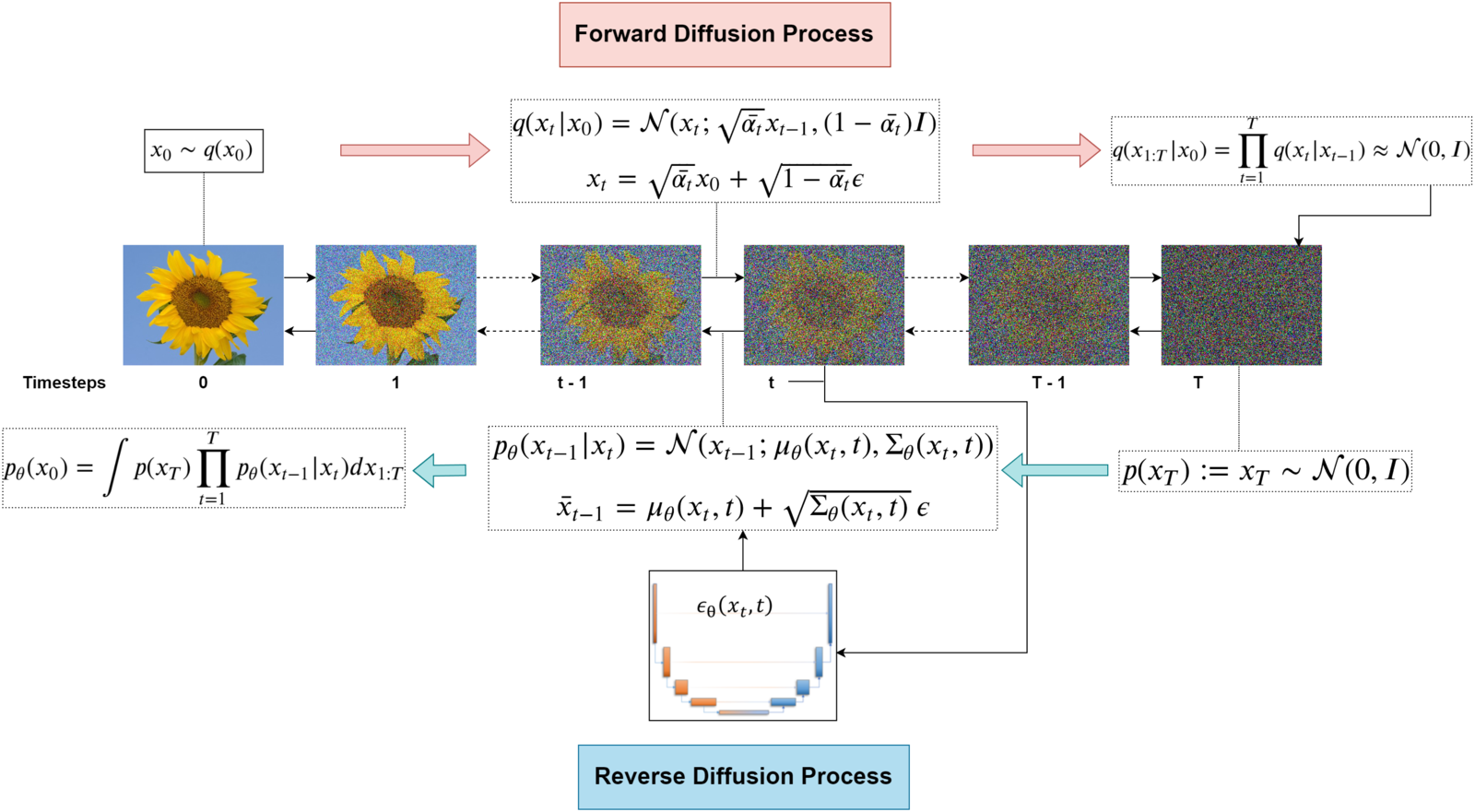
The DDPM class implements a Denoising Diffusion Probabilistic Model, following the original formulation by Ho et al. (2020). It is designed for image generation through iterative denoising of Gaussian-noised data.

This implementation is modular and supports custom noise prediction models and diffusion schedules, while defaulting to a U-Net and linear Gaussian \(\beta\)-schedule.

Total Parameters: 20,907,649 (Default)

Class Signature¶

class DDPM(
    model: nn.Module | None = None,
    image_size: int = 32,
    channels: int = 3,
    timesteps: int = 1000,
    diffuser: nn.Module | None = None,
    clip_denoised: bool = True,
)

Parameters¶

model (nn.Module | None): The noise prediction model \(\epsilon_\theta(\mathbf{x}_t, t)\). If not given, a default UNet is used.

Required forward signature:
```
def forward(self, x: Tensor, t: Tensor) -> Tensor
```
where x is of shape (N, C, H, W) and t of shape (N,).
image_size (int): Size of the (square) input image.
channels (int): Number of channels in the input image.
timesteps (int): Total number of diffusion steps. Controls the length of the forward/reverse process.

diffuser (nn.Module | None): Module implementing the diffusion process. If not provided, defaults to GaussianDiffuser.

Required methods in diffuser:

def sample_timesteps(self, batch_size: int) -> Tensor
def add_noise(self, x_start: Tensor, t: Tensor, noise: Tensor) -> Tensor
def denoise(self, model: nn.Module, x: Tensor, t: Tensor, clip_denoised: bool) -> Tensor

clip_denoised (bool): Whether to clip final denoised outputs to [0, 1].

Returns¶

Use the forward method for training loss:

loss = ddpm(x)

loss (Tensor): MSE loss between true and predicted noise in the denoising process.

Sampling is performed using:

samples = ddpm.sample(batch_size)

samples (Tensor): A tensor of shape (N, C, H, W) containing generated images.

Forward Noise Process¶

To diffuse a clean image \(\mathbf{x}_0\), noise is incrementally added:

\[\mathbf{x}_t = \sqrt{\bar{\alpha}_t} \, \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, \quad \epsilon \sim \mathcal{N}(0, \mathbf{I})\]

where \(\bar{\alpha}_t = \prod_{s=1}^{t} \alpha_s\), and each \(\alpha_t = 1 - \beta_t\).

The function diffuser.add_noise() implements this process.

Reverse Denoising Process¶

The model predicts the added noise \(\epsilon_\theta(\mathbf{x}_t, t)\) and reconstructs an estimate of the original image:

\[\hat{\mathbf{x}}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}} \left( \mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \, \epsilon_\theta(\mathbf{x}_t, t) \right)\]

Then, a new sample \(\mathbf{x}_{t-1}\) is drawn:

\[\mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(\mathbf{x}_t, t) \right) + \sigma_t \mathbf{z}\]

with \(\mathbf{z} \sim \mathcal{N}(0, \mathbf{I})\) and \(\sigma_t^2 = \text{posterior\_var}_t\).

Training Objective¶

DDPM is trained using a noise prediction loss:

\[\mathcal{L}_{\text{simple}} = \mathbb{E}_{\mathbf{x}_0, t, \epsilon} \left[ \left\| \epsilon - \epsilon_\theta(\mathbf{x}_t, t) \right\|^2 \right]\]

Implemented via the DDPM.get_loss() method.

Methods¶

DDPM.get_loss(x: Tensor) → Tensor¶

DDPM.sample(batch_size: int) → Tensor¶

Examples¶

import lucid
import lucid.nn as nn
from lucid.models.imggen import DDPM

model = DDPM(image_size=32, timesteps=1000)

# Training
x = lucid.rand(32, 3, 32, 32)
loss = model(x)
loss.backward()

# Sampling
with lucid.no_grad():
    samples = model.sample(batch_size=16)

Tip

model can be any neural network predicting noise from (x_t, t). It must broadcast t into (N, 1, 1, 1) to match x’s spatial dims.

Warning

Diffusion is sensitive to the beta schedule. Linear schedules like \(\beta_t \in [1e-4, 0.02]\) work well, but others (e.g. cosine) may improve sample quality at fewer steps.